Характеристические уравнения

Принцип действия триггеров уже был описан словесно, таблицами истинности и временными диаграммами. Схемы, включающие в себя триггеры, должны быть удобны в расчетах. Желательно, чтобы триггерами можно было оперировать с помощью алгебры логики. Так как таблицы истинности триггеров известны, то из них можно вывести уравнения алгебры логики. Эти уравнения называются характеристическими уравнениями.
Характеристическое уравнение описывает работу триггера в виде уравнения алгебры логики.
Для каждого вида триггеров можно вывести соответствующее характеристическое уравнение. Оно содержит наряду с входными и выходными переменными величинами указание на два момента времени — tut
п + Г
tn — момент времени перед рассматриваемым тактом.
— момент времени после рассматриваемого такта.
Для начала выведем характеристическое уравнение управляемого по одному фронту /А'-триггера. Его таблица истинности изображена на рис. 7.93.
Эту таблицу истинности нужно преобразовать в полную таблицу истинности. Полные таблицы истинности рассматривались подробнее в разд. 7.4. Они содержат величину Qx в момент времени tn. Получаются восемь возможных случаев (рис. 7.94), которые мы рассмотрим.
В случае 1 (/= О, К= 0) Qx перед тактом равен 0. После такта Qx снова равен 0. В случае 2 (/ = 0, К = 0) Qy перед тактом равен 1 и после такта также равен 1. В случаях 1 и 2 триггер работает в режиме хранения. Выходные состояния не изменяются.
Рис. 7.93. Условное обозначение и таблица истинности управляемого по одному фронту /АТ-триггера.

В случае 3 (/ = 1, К = 0) до такта Qt = 0. Управляющим синхроимпульсом он будет установлен в 1. После такта Q, = 1. В случае 4 (/= 1, К = 0) Q, перед тактом 1. Итак, триггер уже предустановлен. Управляющий синхроимпульс не вызывает никаких изменений. Qx остается на 1. В случаях 3 и 4 триггер работает в режиме установки. Какое бы состояние ни имел Q, перед тактом, после такта всегда Q, — 1. Триггер устанавливается.
В случае 5 (J = 0, К = 1) до такта Qt = 0. Триггер должен сброситься. Однако так как он уже сброшен, то состояние выхода Qx с приходом такта синхроимпульса не изменится. В случае 6 (/ = 0, К = 1) до такта Qt = 0. Триггер установлен перед тактом. Управляющим синхроимпульсом он будет сброшен в Qx = 0. В случаях 5 и 6 триггер работает в режиме сброса. Какое бы состояние ни имел Q, перед тактом, после такта всегда Q{ = 0. Триггер сбрасывается.
В случае 7 (J — 1, К = 1)до такта Q{ = 0. С приходом управляющего синхроимпульса выход должен переключиться в противоположное состояние. Следовательно, после такта Qt = 1. В случае 8(/=1,А'=1)до такта 0{ = 1. С приходом управляющего синхроимпульса выход переключается в противоположное состояние. Следовательно, после такта Ql = 0. В случаях 7 и 8 триггер работает в режиме инверсии.
Из полной таблицы истинности получается нормальная форма ИЛИ (см. разд. 5.2.1). В случаях 2, 3, 4 и 7 к моменту времени tn + , Qx = 1. Получаются четыре полные конъюнкции (см. рис. 7.94). Нормальная форма ИЛИ:
Переменные К, J и Q{ перед рассматриваемым тактом получают индекс п. Переменная Q, после рассматриваемого такта получает индекс п + 1. Она записывается Qt (и +1}.
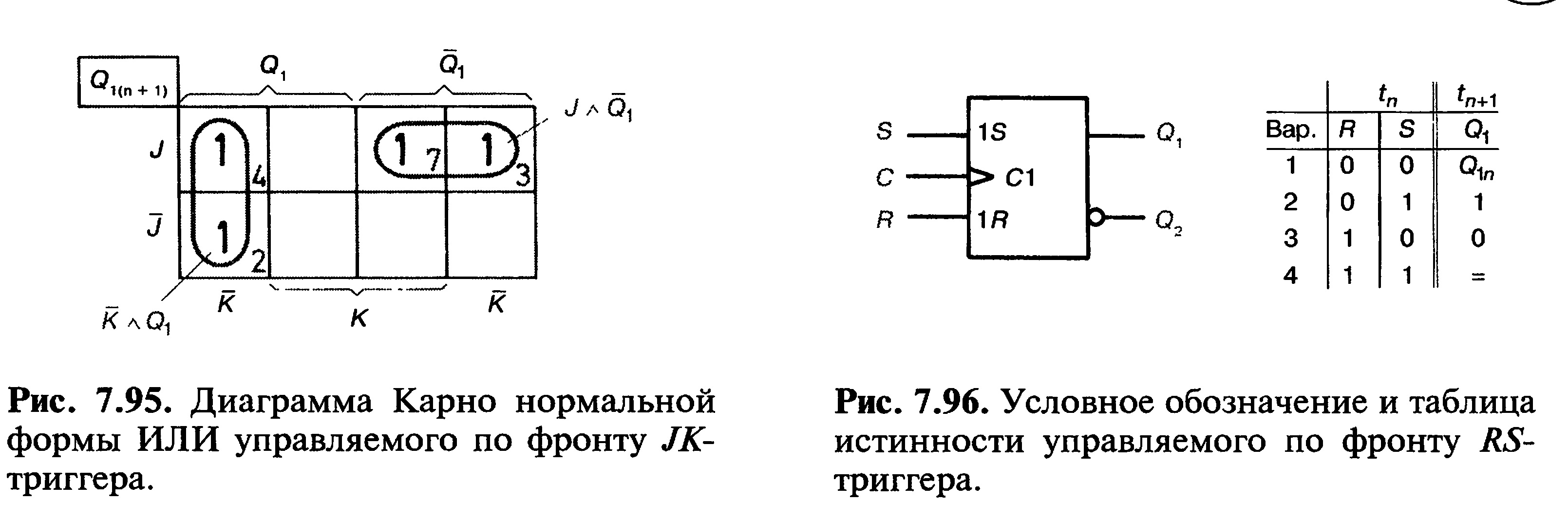
Найденная нормальная форма ИЛИ может быть упрощена с помощью алгебры логики или диаграммы Карно (см. разд. 5.4). Соответствующая диаграмма Карно показана на рис. 7.95. Из диаграммы можно определить упрощенное уравнение:
Это уравнение является характеристическим уравнением управляемого по фронту /^-триггера. Для уравнения не имеет значения, передний или задний фронт синхроимпульса переключает триггер. Характеристическое уравнение имеет силу для обоих видов управляемых по одному фронту
С1(я+1) = [(<2, А/ А К) V (0, А / Л К) V ^ А / А К) V (Q, A J Л *)].
= [(J Л v {к л О,)]. (JK-триггер)

Оно имеет силу также для управляемых по двум фронтам триггеров, так как время tn и tn + l является моментом времени до и после такта, а не фронта.
Теперь выведем характеристическое уравнение управляемого по фронту &У-триггера. Таблица истинности в обыкновенной форме показана на рис. 7.96. Таблица истинности преобразуется в полную таблицу истинности (рис. 7.97).
Из полной таблицы истинности получается нормальная форма ИЛИ:
б1(и + 1) = [(0! A s A R) V (б, A S A R) V ((?, A S А .
Нормальная форма ИЛИ упрощается с помощью диаграммы Карно (рис. 7.98). Получается следующее характеристическое уравнение:
Q1,„tlJ=[RA(SA01)]„
(RS-триггер)
Мы пропустили запрещенные случаи 7 и 8 на рис. 7.97 при выводе характеристического уравнения. Эти случаи можно учесть в диаграмме Карно.
В случаях 7 и 8 Ql(n + может принимать значения как 0, так и 1.
В клетках комбинаций 7 и 8 вместо соответствующих полных конъюнкций вставлены крестики (рис. 7.99). В случае 7 полная конъюнкция была
бы Qx a S a R. Вместо нее стоит крест. Полная конъюнкция в случае 8 была бы Qj a S a R. И на ее месте стоит крест.

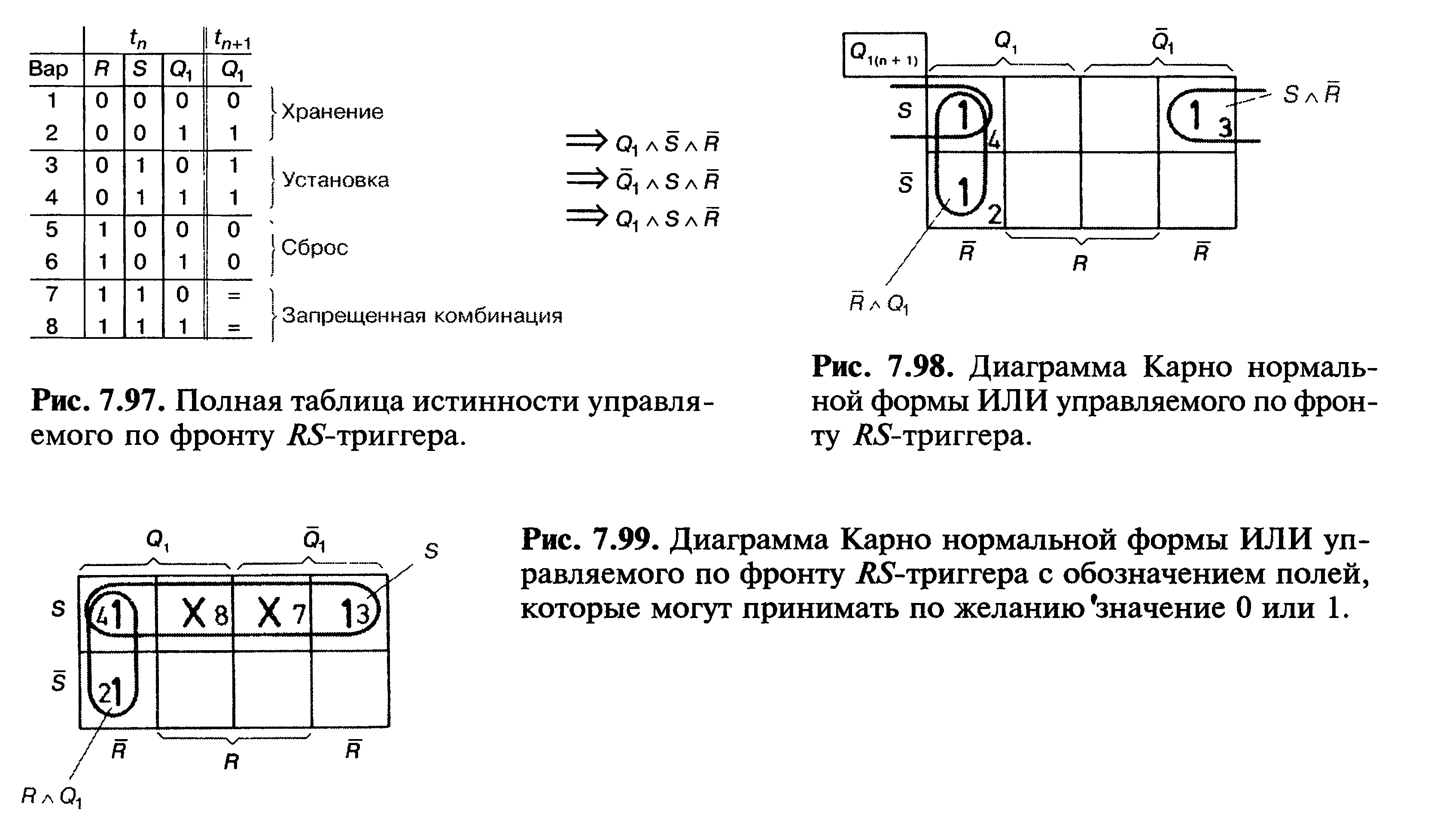
Клетки в диаграмме Карно, которые обозначены крестом, могут быть по желанию рассмотрены как 0 или 1.
Из ячеек с крестами можно образовывать группы. Благодаря этому уравнения упрощаются. Для диаграммы Карно на рис. 7.79 получается характеристическое уравнение:
(RS-триггер)
Как выглядит характеристическое уравнение управляемого по фронту Г-триггера с Г и С входами? На рис. 7.100 указаны таблица истинности и условное обозначение. По таблице истинности можно построить полную таблицу истинности (рис. 7.101). Нормальная форма ИЛИ:

Карта Карно на рис. 7.102 показывает, что дальнейшее упрощение нормальной формы ИЛИ невозможно. Характеристическое уравнение управляемого по фронту Г-триггера:
0„„„, =[(0,a7)v(0, лг)]^
(Г-триггер)
Для триггеров, управляемых по уровню сигнала также можно определить характеристические уравнения. Характеристическое уравнение управляемого по фронту ^-триггера совпадает с характеристическим уравнением управляемого по уровню тактового сигнала ^-триггера.

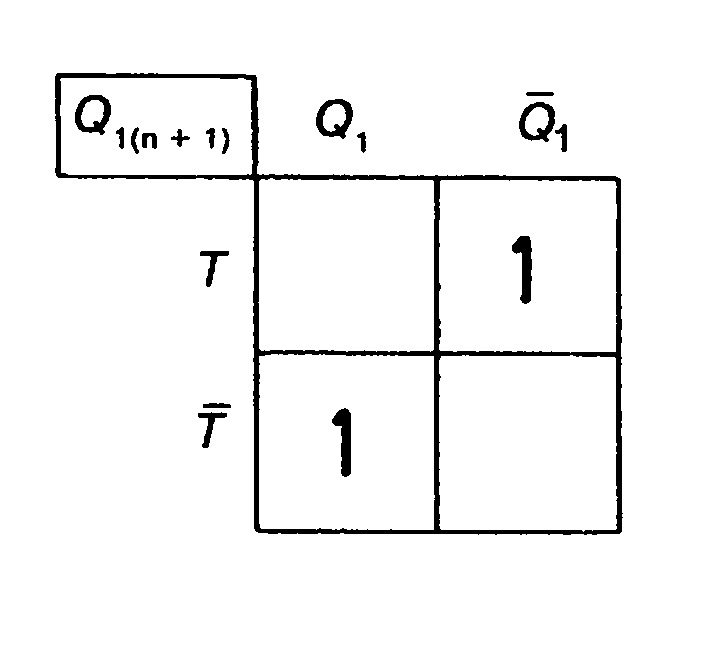
Рис. 7.102. Диаграмма Карно нормальной формы ИЛИ управляемого по фронту T-триггера

Так получается, потому что моменты времени tn и tn + у являются моментами до и после рассматриваемого такта синхронизации. Собственно сам момент переключения, который виден на временной диаграмме, характеристическое уравнение не рассматривает.
Полученные характеристические уравнения управляемого по одному фронту триггера действительны для триггера, тактируемого по уровню сигнала того же вида.
Принцип действия нетактируемых триггеров можно описать характеристическим уравнением. Только временные точки нужно определить иначе. Момент времени tm является рассматриваемым моментом времени, в который на входах и выходах действуют записанные в таблице истинности сигналы. Момент времени tm _ х является предыдущим моментом времени с другими входными сигналами.
Условное обозначение и таблица истинности для триггера из двух элементов И-НЕ приведены на рис. 7.103. Полная таблица истинности и диаграмма Карно показаны на рис. 7.104. Получается следующее характеристическое уравнение:

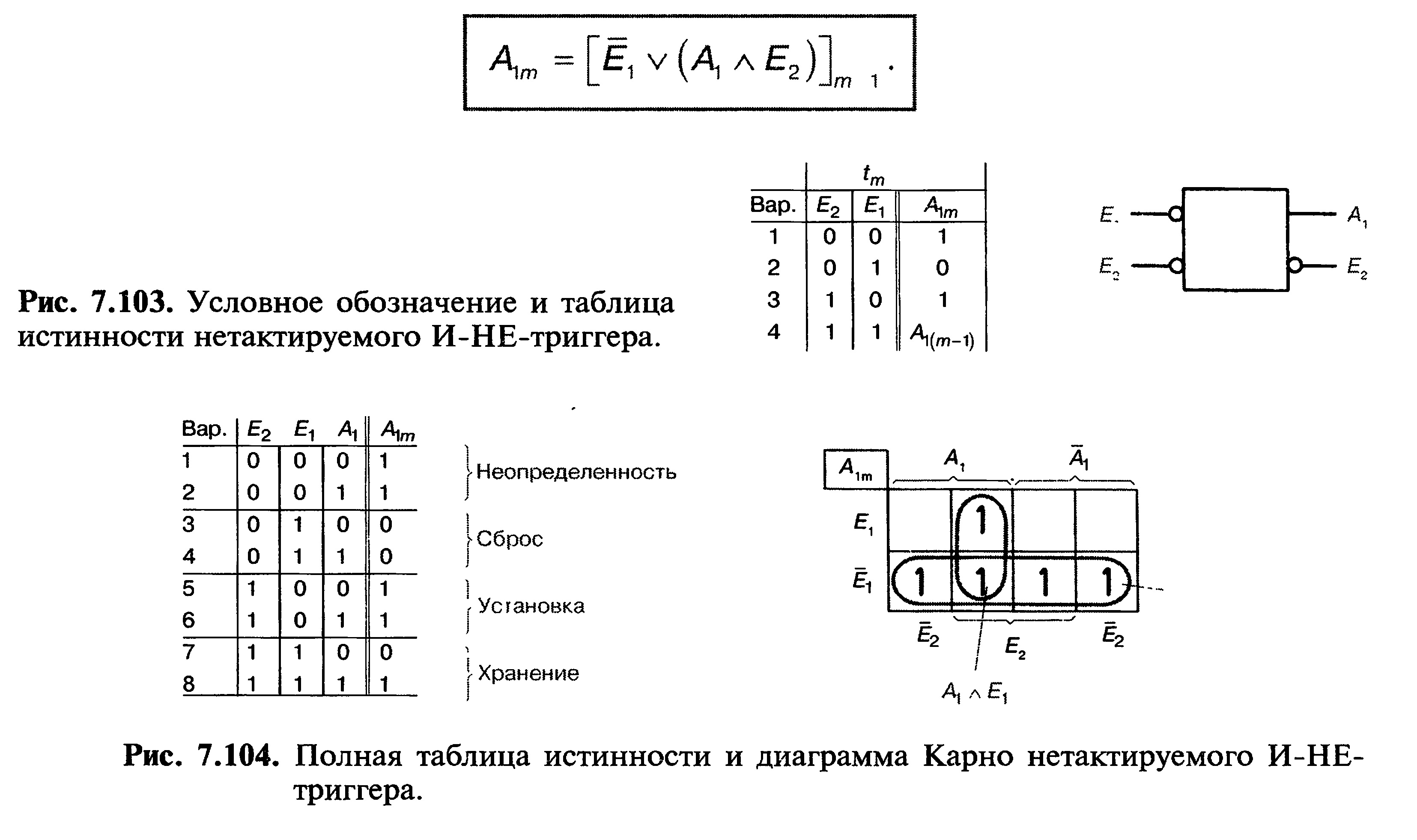
С помощью характеристических уравнений можно рассчитывать схемы, содержащие триггеры и логические элементы (см. гл. 11).

Похожие статьи