Комбинированные элементы

Логический элемент «И-НЕ»

Если соединить последовательно элементы «И» и «НЕ» согласно схеме на рис. 2.11, то выход Xлогического элемента «И» инвертируется согласно таблице истинности (рис 2.12). В колонке Xприведен выходной сигнал элемента «И» равен 1 только если А = 1 и В = 1 (вариант 4). В свою очередь X является входом для инвертора. Если на входе X элемента НЕ логическая 1, то выход Z = 0. Если на входе X элемента НЕ логический 0, то выход Z = 1.

В колонке Z приведен инвертированный выход X элемента И.

В англоязычной литературе такой комбинированный элемент обозначается как NAND (сокр. от NOT + AND).

Вентили «И-НЕ» используются очень часто. Для них придумали собственное условное обозначение (рис. 2.13). Оно получается из символа вентиля «И» с кружком на выходе. Этот кружок означает инвертирование выхода. Для логического элемента «И-НЕ» действительно следующее утверждение:

На выходе логического элемента «И-НЕ» логическая 1 будет только в том случае, если не на всех входах наступает состояние 1.

Рис. 2.13. Условные обозначения «И-НЕ»-элементов с двумя входами

Логическая функция элемента «И-НЕ» отвечает выражению:

Z = AaB.

Длинная черта над А а В указывает, что инвертируется все выражение.

Таблица истинности элемента «И-НЕ» приведена на рис. 2.14.

Логический элемент ИЛИ-НЕ

Таблица истинности соединенных последовательно элементов ИЛИ и НЕ согласно схеме на рис. 2.15 приведена на рис 2.16. Сначала входные сигналы А и В поступают на вентиль ИЛИ:

Х= A v В.

X является одновременно входом элемента НЕ. Все состояния X инвертированы в столбце Z (из X = 0 будет Z = 1, из X = 1 будет Z— 0).

Выход Z является выходом элемента ИЛИ-HE. В англоязычной литературе такой комбинированный элемент обозначается как NOR (сокр. от NOT + OR).

Логические элементы ИЛИ-HE используются так же часто, как и элементы И-НЕ. Для них так же создано собственное условное обозначение (рис. 2.17). Оно получается из символа вентиля ИЛИ с кружком на выходе. Этот кружок означает инвертирование выхода.

Для логического элемента ИЛИ-HE действительно следующее утверждение:

На выходе логического элемента ИЛИ-HE логическая 1 будет только в том случае, если ни на одном из входов нет состояния 1.

Логическая функция элемента ИЛИ-HE отвечает выражению:

Z - A v В.

Рис. 2.17. Условные обозначения ИЛИ-НЕ-элементов с двумя входами

 

Логический элемент эквивалентности

Часто возникает необходимость в схемах, в которых на выходе всегда логическая 1, когда на оба входа поданы одинаковые логические сигналы — либо оба 0, либо оба 1. Такая схема называется логическим элементом эквивалентности (эквивалентность — равноценность). Она строится из основных логических элементов соответственно (рис. 2.18).

Разберем подробно таблицу истинности эквивалентного элемента. Сначала для четырех возможных комбинаций записываются логические состояния входов А и В (рис. 2.19, столбцы © и ©). Затем они инвертируются элементом НЕ, превращаясь в А и В. Если /1 = 0, то соответственно А = 1. Если, как в случае 4, А = 1, то соответственно А = 0. Такое же правило действует и для В и В. Так получают содержимое столбцов ® и © на рис. 2.19. Состояние выхода Q получается из операции логического умножения А и В. В случае 1 А = 0, В = 0, следовательно, Q должен быть также равен 0 (столбец ©). В случаях 2 и 3 Q равен также 0, так как оба входа не являются логической 1. Только в случае 4, где А=1тВ=1, Q также равен 1.

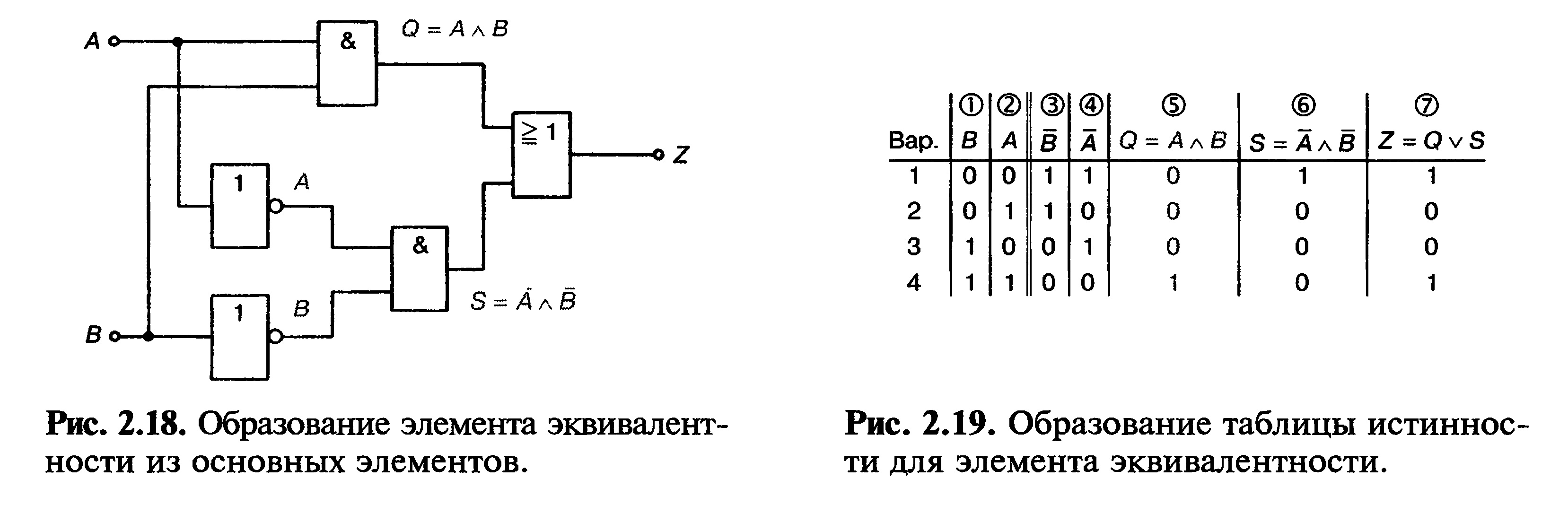
Символом S в колонке 6 обозначается результат логического умножения А и В. А и В являются входами логического элемента ИЛИ с выходом S (рис. 2.18). В первом случае А = 1 и В = 1. Следовательно, для первого случая S = 1. В случаях 2 и 3 таблицы истинности S = 0, так как только один из входов имеет состояние 1. В случае 4 оба входа равны 0 и соответственно S = 0.

S и Q являются выходами обоих элементов И и одновременно входами элемента ИЛИ. Логический элемент ИЛИ производит операцию логического сложения состояний и Q. В случае 1 Q = 0 и 1. Следовательно, на выходе Z(столбец ©) также 1. В случаях 2 и 3 оба входа 0, и таким образом, на выходе также 0. В случае 4 Q = 1 и 5 = 0, что при операции сложения дает результат 1.

Для элементов эквивалентности также создано собственное условное обозначение. Условное обозначение и таблица истинности приведены на рис. 2.20.

На выходе элемента эквивалентности состояние 1 будет только тогда, когда входы имеют равное состояние.

Логическая функция элемента эквивалентности отвечает выражению:

Z = (AaB)v(AaB)

Так как в нашем примере Q = А д В и

S = А л В, можно также записать Z— Qv S. Элемент эквивалентности можно построить и из других основных логических элементов (см. задания в конце гл. 2).

Логический элемент ИСКЛЮЧАЮЩЕЕ ИЛИ (XOR)

Если выход элемента эквивалентности инвертируется посредством последовательного подключения элемента НЕ, то возникает элемент, который на выходе всегда имеет 1, если его входы различны (рис. 2.21).

Такой элемент называется элементом ИСКЛЮЧАЮЩЕЕ ИЛИ. Речь идет при этом об элементе ИЛИ, в котором исключен случай, когда на выходе находится 1, если оба входа имеют 1 (случай 4). В англоязычной литературе такой элемент обозначается как XOR (сокр. от EXCLUSIVE + OR).

Логические элементы ИСКЛЮЧАЮЩЕЕ ИЛИ используются достаточно часто. Условное обозначение и таблица истинности приведены на рис. 2.22.

На выходе элемента ИСКЛЮЧАЮЩЕЕ ИЛИ состояние 1 будет только тогда, когда оба входа имеют различное состояние.

Логическая функция элемента эквивалентности может быть получена из схемы на рис. 2.21:

X = (AaB)v(AaB).

Тогда логическую функцию элемента ИСКЛЮЧАЮЩЕЕ ИЛИ можно представить как инверсию логической функции элемента эквивалентности:

Z = (А л В) v (А а е)

Это выражение можно преобразовать с помощью правил алгебры логики:

Z = (Л А Б) V (Д А В)

Правила преобразования подробно рассматриваются в гл. 4.

Рис. 2.22. Условное обозначение XOR-элемента и его таблица истинности

 

Комбинации элементов с двумя входами

После рассмотрения элементов И, ИЛИ, НЕ, ИЛИ-HE, И-НЕ, ЭКВИВАЛЕНТНОСТИ и ИСКЛЮЧАЮЩЕГО ИЛИ посмотрим варианты дальнейших возможных комбинаций и соответствующие им элементы. Существует еще много вариантов соединения, но они не имеют большого практического значения.

Для элементов с двумя входами (например А и В) возможны 4 различных варианта (комбинаций) входов, как мы видели в рассмотренных до сих пор таблицах истинности (см. рис. 2.22). Для этих 4 вариантов возможны 4 возможных варианта на выходе, например выход Zна рис. 2.23. В каждом из серых квадратиков может быть выходное состояние 0 или 1.

Рис. 2.23. Таблица истинности для элементов с двумя входами. Серые квадраты для возможных состояний выходов.

Можно составить 16 различных комбинаций выходных состояний. Они обозначены на рис. 2.24 от Zy до Z16. Из рисунка сразу становится ясно, что некоторые из возможных комбинаций не имеют особого значения. Для «константы 0» и «константы 1» не нужно вводить никаких элементов. «Константа 0» означает, что выход всегда равен 0, абсолютно независимо от того, какие состояния на входах. При «константе 1» на выходе всегда 1, также независимо от состояния на входах.

 

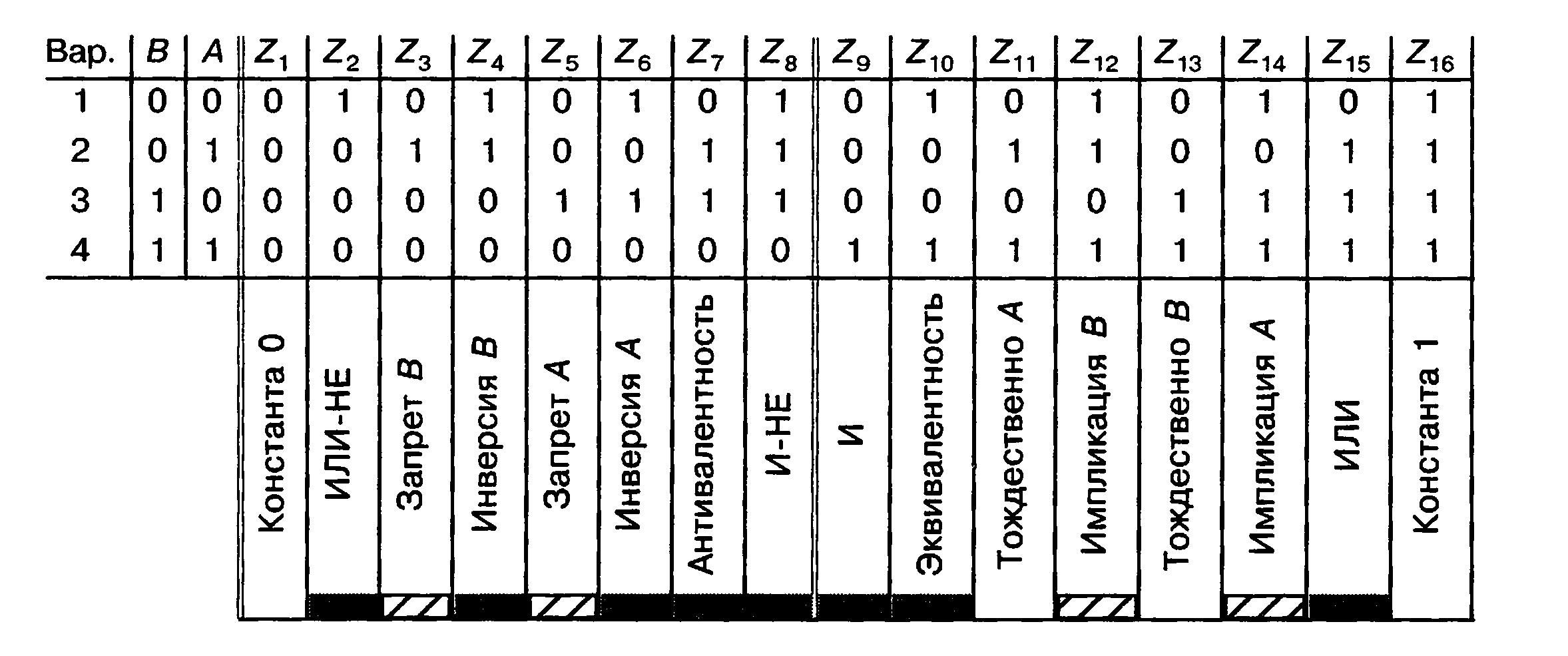
Рис. 2.24. Общая таблица для 16 возможных состояний выходов элементов с двумя входам

«Инверсия А» и «инверсия В» соответственно реализуются логическим элементом НЕ. Для «тождественно А» и «тождественно В» можно использовать не инвертирующий усилитель (рис. 2.25).

На выходе не инвертирующего усилителя только тогда логическая 1, когда на вход подана логическая 1.

Усилители такого рода предназначены для усиления слабых сигналов.

Запрещение является особой разновидностью элемента И. Состояние входа инвертируется перед элементом И. Если инвертируется вход А, то элемент называется схема запрета А (рис. 2.26). Если инвертируется вход В, то элемент называется схема запрета В (рис. 2.27).

Импликация является особой разновидностью элемента ИЛИ. Состояние входа инвертируется перед элементом ИЛИ. Если инвертируется вход А, то элемент называется импликатор А (рис. 2.28). Если инвертируется вход В, то элемент называется импликатор В (рис. 2.29).

 

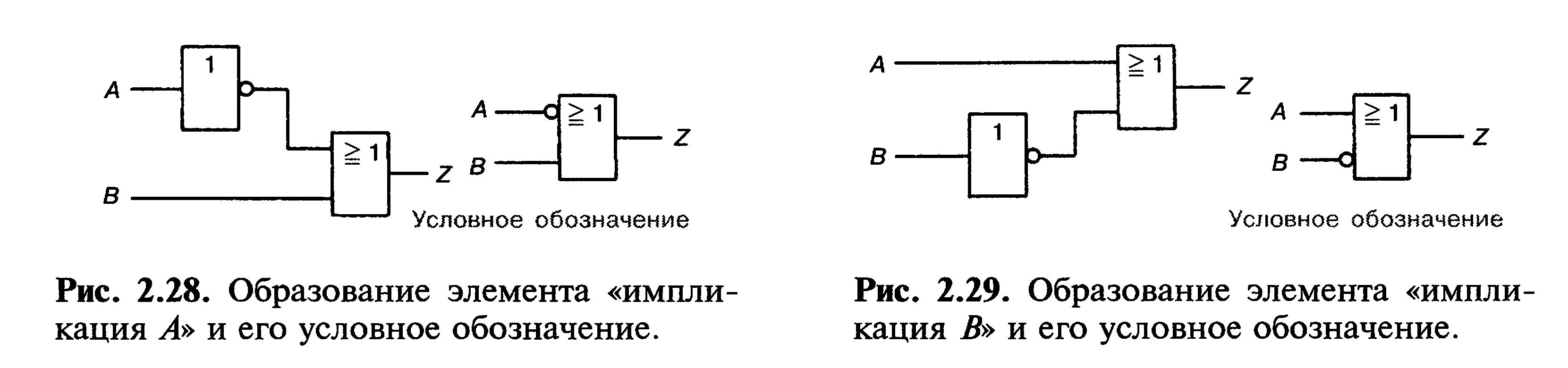
Логические элементы запрещения и импликации имеют ограниченное практическое значение и почти не производятся. В случае необходимости их можно собрать из основных логических элементов.

 

Логические элементы с тремя и более входами

Если необходимы три входа или больше, то можно включить последовательно несколько двухвходовых элементов (рис. 2.30).

Каждый элемент с двумя входами имеет, как известно, 4 возможных комбинаций входов-выходов. Для входов А и В имеет силу обыкновенная таблица истинности. Если добавляется еще один вход, например С, то он может быть либо 0, либо 1.

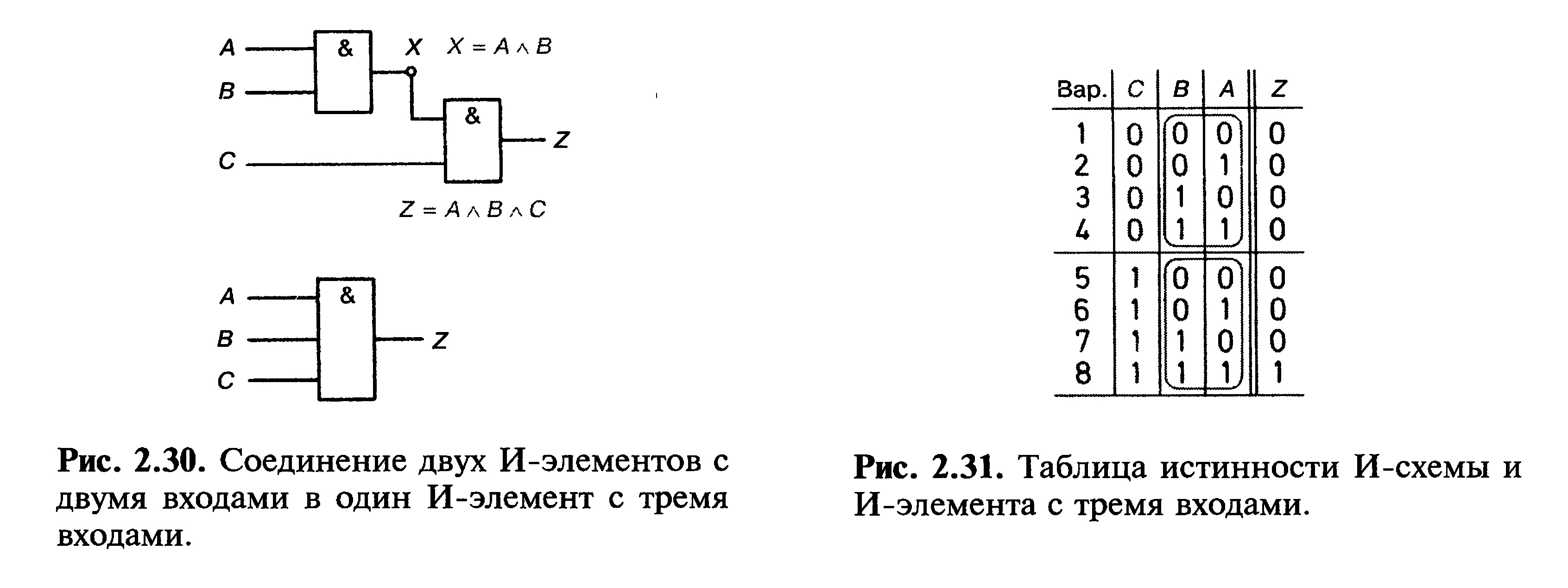
Прежние 4 комбинации от А и В комбинируются один раз с С = 0 и второй раз с С = 1 (рис. 2.31). Таким образом получаются 8 комбинаций. Если теперь к трем входам, например А, В, С добавляют четвертый вход, например D (рис. 2.32), то прежние 8 комбинаций от А, В и С комбинируются один раз с D = 0 и второй раз с D = 1 (рис. 2.33). Член с 4 входами имеет, таким образом, 16 возможных комбинаций (рис. 2.33).

С добавлением каждого нового входа число комбинаций (вариантов вход-выход) таблицы истинности удваивается.

При двух входах — 4 комбинации, при трех входах — 8 комбинаций, при четырех входах — 16 комбинаций и при пяти входах получаются 32 комбинации. При формировании таблиц истинности последовательность комбинаций выбирается произвольно. Нужно учитывать все варианты и не допускать повторов. Чтобы проще было составлять таблицы истинности, предлагаем следующую схему.

Первый вход (например АI) меняет состояние каждый раз. Второй вход (например В) меняет состояние через раз. Третий вход (например С) меняет состояние через 4 варианта. Если продолжать по этой схеме, четвертый вход (например D) меняет состояние соответственно после 8 комбинаций, и так далее. Эта схема оправдала себя на практике. Указанные в данной книге таблицы истинности составлены согласно этой схеме.

Выпускаемые в настоящее время вентили И и ИЛИ имеют в основном от 2 до 4 входов. То же самое относится к вентилям И-НЕ и ИЛИ-НЕ. Изредка встречаются вентили с 8 и более входами.

Контрольный тест

1. Изобразите условное обозначение для вентилей И, ИЛИ, НЕ, И-НЕ и ИЛИ-HE. Все элементы, включая НЕ, должны иметь два входа.

2. Постройте таблицу истинности вентиля ИЛИ с тремя входами. Входы имеют обозначения А, В, С. Выход имеет обозначение Z

3. Предложите вариант построения вентиля И-НЕ из основных логических элементов.

4. Изобразите таблицу истинности элемента НЕ с входом А и выходом Y.

5. Для элемента ИСКЛЮЧАЮЩЕЕ ИЛИ верно уравнение

Z = (AaB)v(A*B).

Синтезируйте его из логических элементов И, ИЛИ и НЕ и нарисуйте схему.

6. Опишите словами функции логических элементов И и ИЛИ.

7. Сколько возможных комбинаций имеет таблица истинности элемента ИЛИ с шестью входами?

8. Что понимают под логическим элементом ИСКЛЮЧАЮЩЕЕ ИЛИ? Изобразите для этого элемента таблицу истинности.

9. Как называется логический элемент, которому соответствует таблица истинности, изображенная на рис. 2.34?

10. Какую функцию выполняет элемент ЗАПРЕЩЕНИЕ? Как его можно построить из основных логических элементов? Нарисуйте возможную схему.

11. Временные диаграммы входов А и В представлены на рис. 2.35 Изобразите временную диаграмму выхода Z, если А и В входы

а) вентиля И,

б)           вентиля ИЛИ.

 

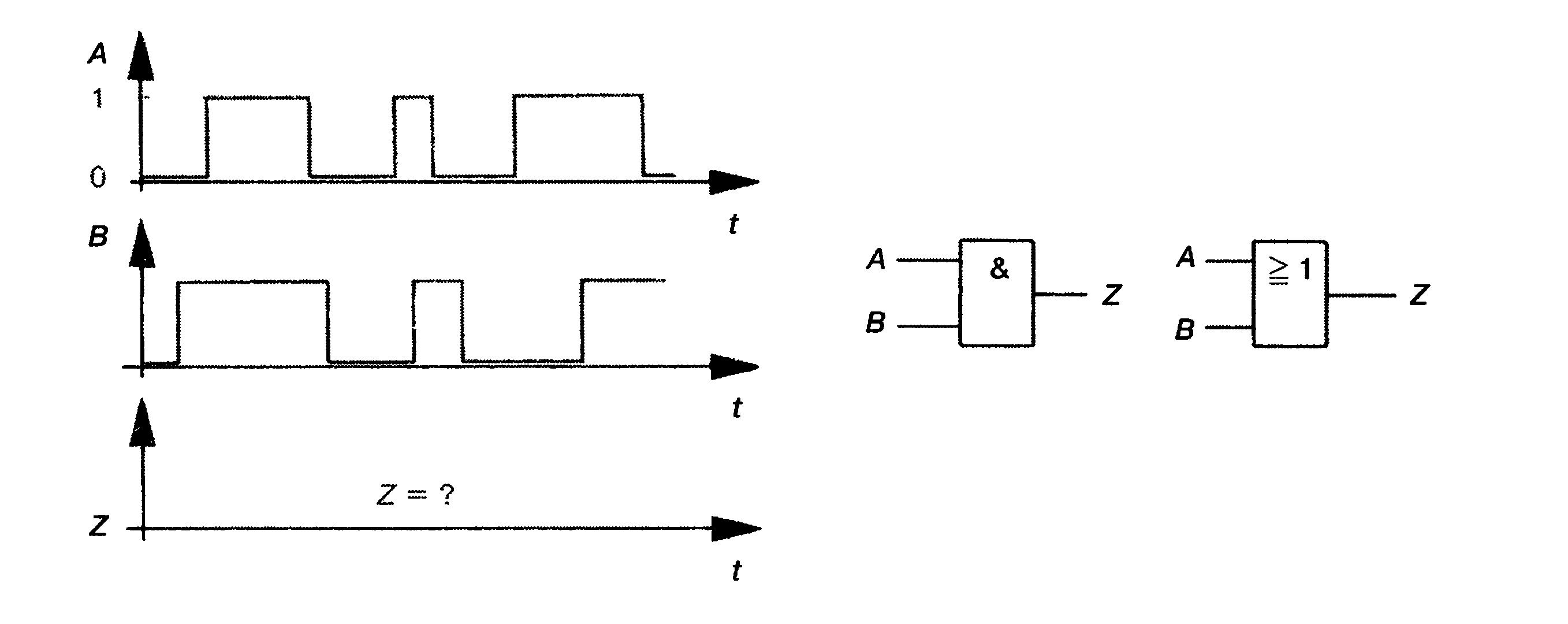
Рис. 2.35. Связь двух входных сигналов А и В

12.          Какую логическую операцию производят элементы на схеме рис. 2.36?

Рис. 2.36. Комбинация логических элементов.

13. Изобразите таблицу истинности элемента НЕ с пятью входами. Входы обозначить как Ev Ev Ev Е4 и Еу Выход обозначить как X.

14. На рис. 2.37 представлены входные сигналы А и В и выходной сигнал Z неизвестного элемента. Какую логическую операцию производит этот член?

 

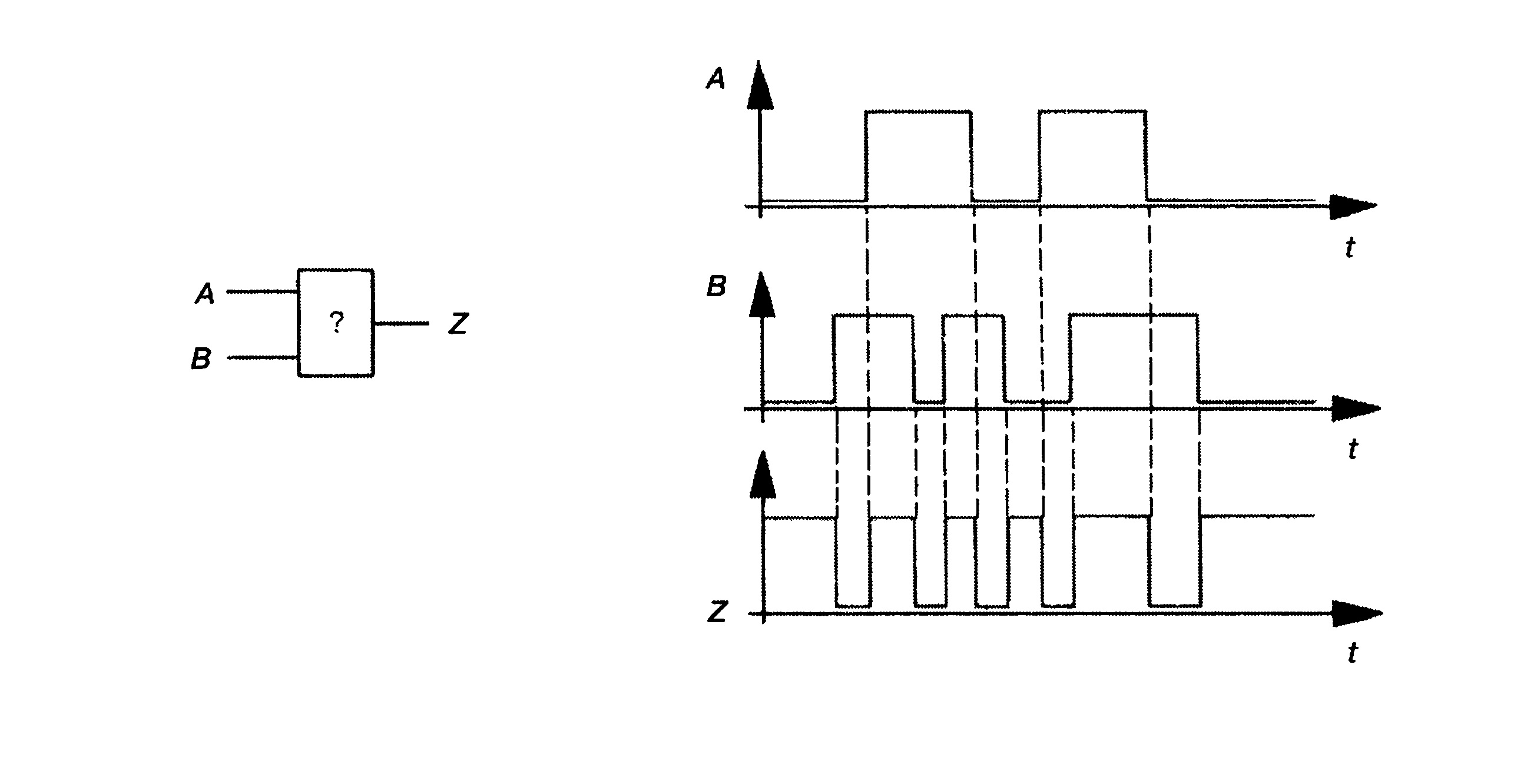
Рис. 2.37. Временные диаграммы входов и выхода

Похожие статьи