Логические функции и цифровые схемы

Определение логической функции цифровой схемы

Логическая функция цифровой схемы может быть записана в виде таблицы истинности. Отдельные шаги при составлении таблицы истинности ведут к итоговому уравнению для выхода всей схемы, в котором присутствуют только состояния входов или их инвертированные состояния (см. подразд. 2.1.2). Такое уравнение выражает функцию всей схемы. Поэтому оно называется логической функцией цифровой схемы.
Для каждой цифровой схемы существует логическая функция.
Уравнение функции может быть найдено из анализа цифровой схемы. Для его составления не требуется восстанавливать таблицу истинности.
Цифровая схема (рис. 3.6) состоит из элементов с I по V. Если обозначить вход элемента / как А, то на выходе получится А. Входы элемента II обозначим А и С. Выход обозначим как М:
М= А л С.
Входами элемента IIIявляются А, В и С. Выход обозначим как К:
К = А л ВлС.
М и К являются входами элемента IV, над которыми производится логическое сложение. Выход элемента IV обозначим X:
Х= Kv М.
В это уравнение могут быть подставлены уже известные выражения для КиМ:
Х= К v М
X = {АлВлС)ч(АлС).
X является также входом элемента V. Так как элемент V инвертирует состояние X, то
Z = X
и
Z = (А а В а С) v (А л С)
так как X = [А л В (А л С).

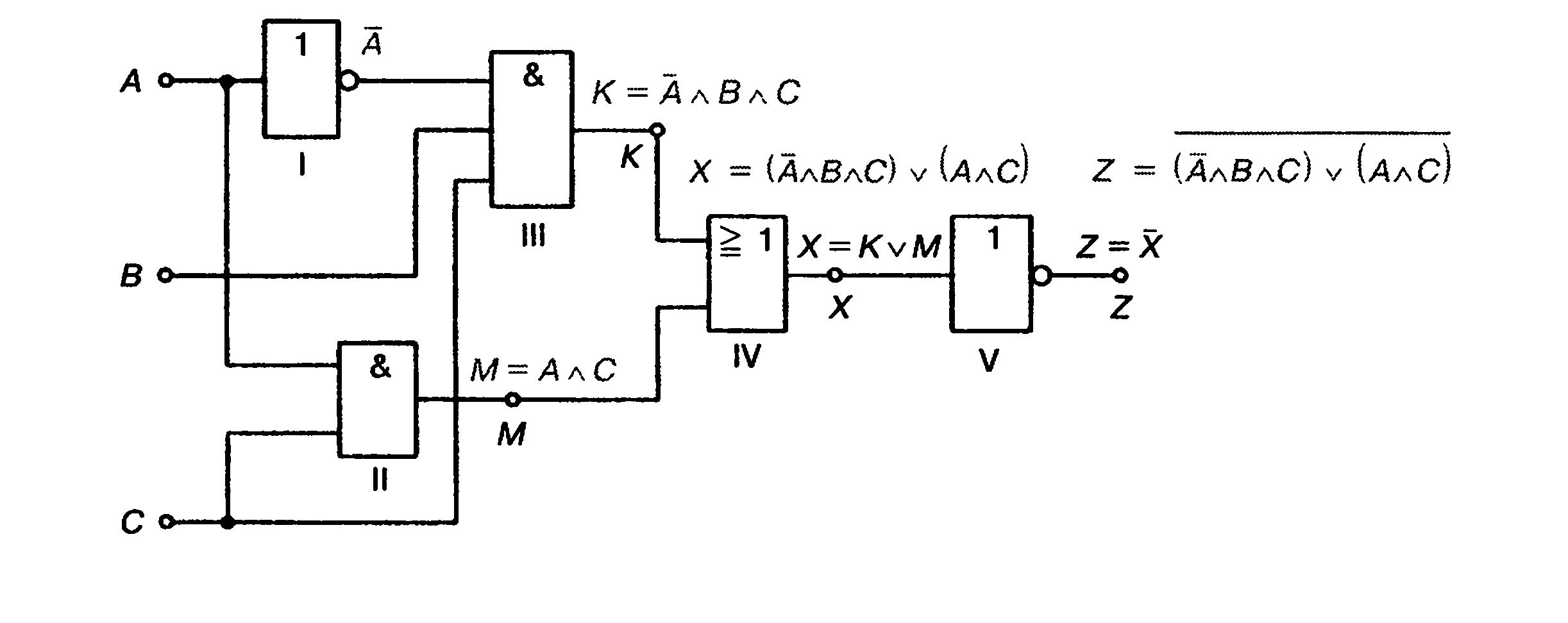
Рис 3.6. Цифровая схема

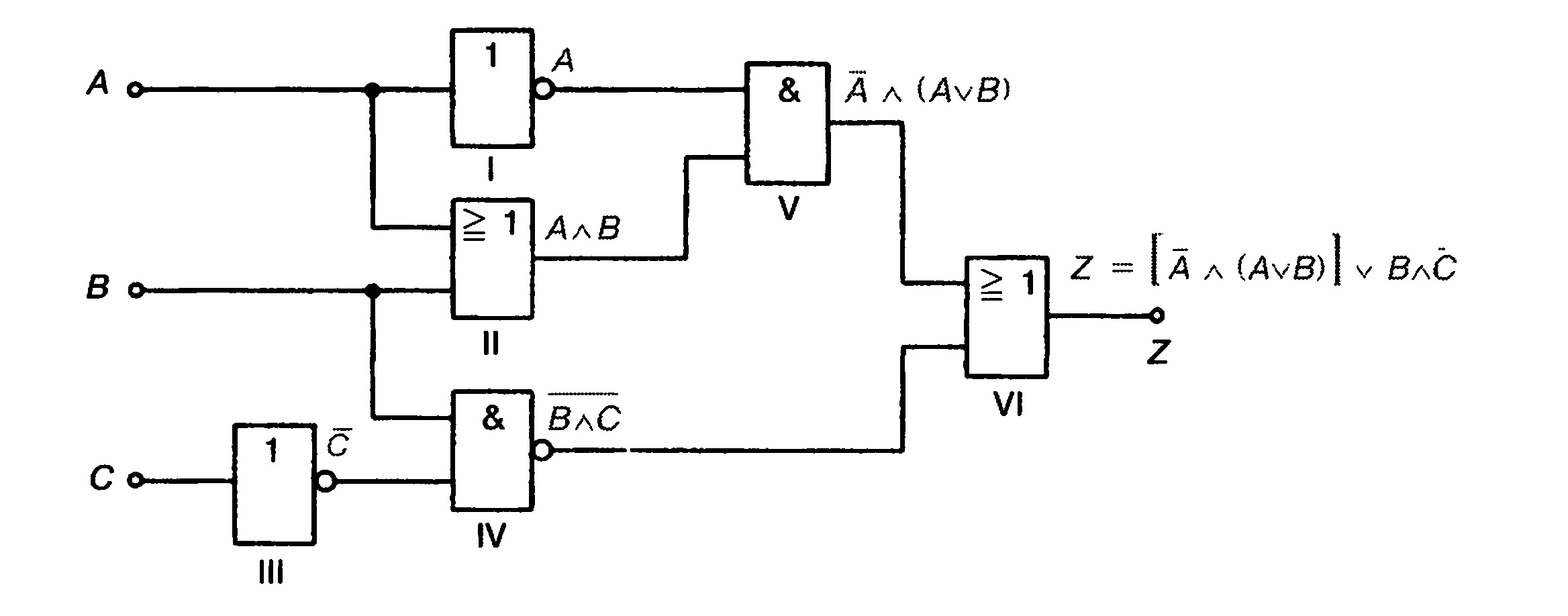
Рис 3.7. Цифровая схема

Уравнение для Z является искомой логической функцией схемы.
Если пройти еще раз по цепочке рассуждений, то можно не употреблять обозначения К, М и X в рассмотренном примере. Входы можно также обозначать, например как (А л С), то есть в виде логического выражения. Найдем уравнение логической функции для схемы рис. 3.7.
На выходе элементов записываются логические выражения, то есть на
выходе элемента I — Л, на выходе элемента II — A v В и т. д. Эти выражения являются одновременно входами следующих элементов. Элемент IV
имеет входы С п В. На выходе после операции логического сложения оказывается состояние В а С. Так как элемент IVявляется вентилем И-НЕ, то все выражение еще раз инвертируется, так что на выходе получается В д С. На выходе элемента Vбудет состояние А а (А v В), так как его входами
являются А и A v В.
Выражения, относящиеся друг к другу, должны всегда ставиться в скобки. В гл. 4 («Алгебра логики») говорится, что согласно правилам операция логического умножения И имеет более высокий приоритет, чем операция логического сложения ИЛИ, то есть выполняется первой. Поэтому на всякий случай нужно всегда ставить скобки — по крайней мере первое время. Линия инверсии рассматривается и действует так же, как скобки.
Вход элемента VI обозначен выражением А а (А v В). Это выражение должно быть заключено в скобки. Второй вход элемента VI обозначен выражением В а С. Здесь скобки не требуются, так как общая черта отрицания их заменяет.
Для Z получается следующее уравнение:
Z = [Aa(AvB)]vBaC.
Это уравнение является искомой логической функцией цифровой схемы.
Предположим, что элементом VI на рис. 3.7 будет элемент ИЛИ-НЕ. Как будет тогда выглядеть логическая функция схемы? Найденная для Z функция вся подвергается инверсии (отрицанию). Это указывается чертой отрицания над всем выражением:
Z = [Aa(AvB)]vBaC.
Получившееся уравнение выглядит сложнее, чем является в действительности.

Синтез схемы по заданной логической функции

На практике часто бывает, что логическая функция получается в результате вычислений и требуется синтезировать схему, реализующую данную функцию.
Для уравнения
Z = ^v5vCv(i4vCj
требуется синтезировать цифровую схему.
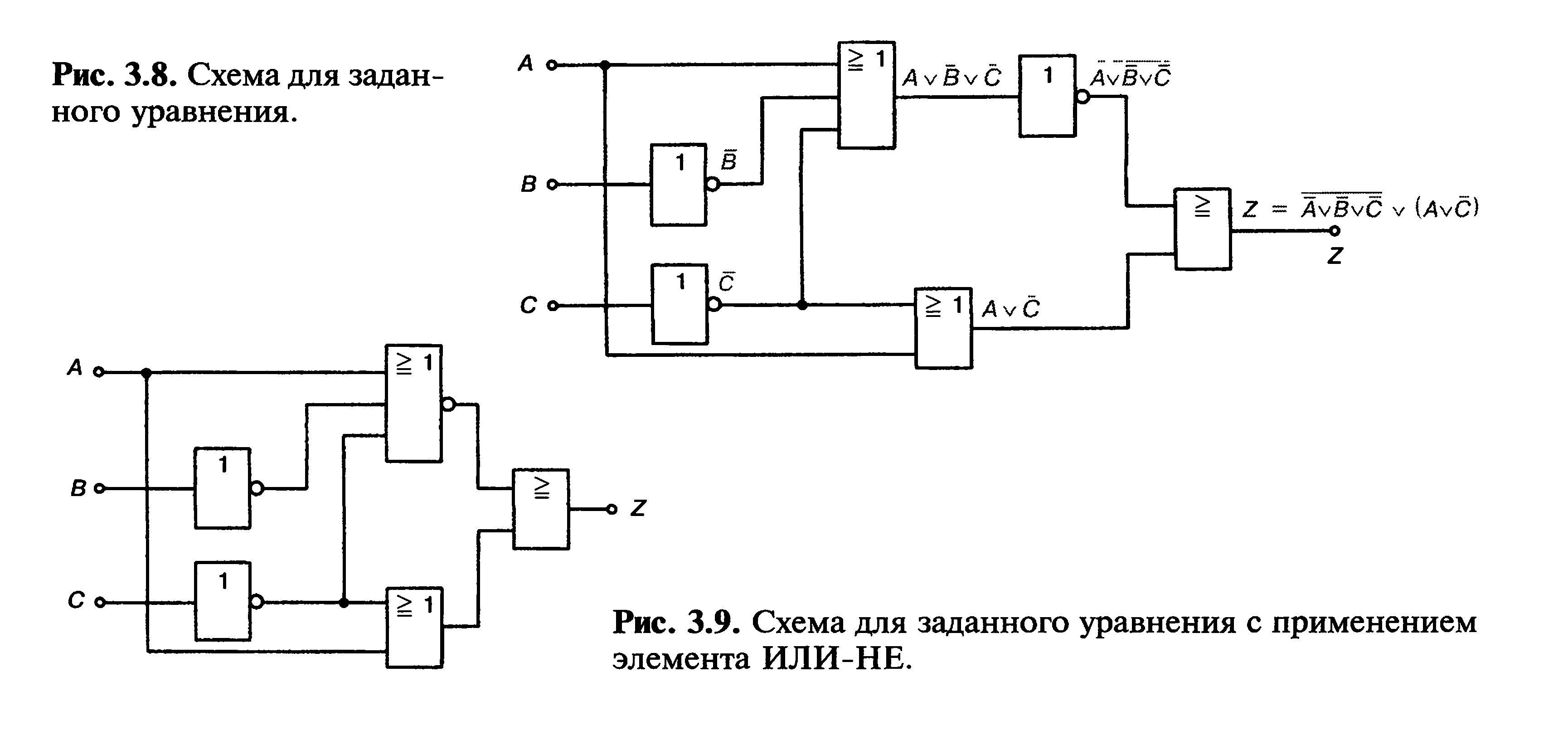
Сначала нужно определить из уравнения число входов. Входами являются А, В и С. Для получения В и С необходимы два элемента НЕ (рис. 3.8).
Выражение A v В v С получают при помощи элемента ИЛИ с тремя входами. К этому элементу последовательно подключается элемент НЕ.
Для (A v С) требуется элемент ИЛИ с двумя входами. Выходы с состояниями AvBvC и (A v С) поступают на вход элемента ИЛИ.
Вместо элемента ИЛИ с тремя входами и последующим вентилем НЕ можно использовать элемент ИЛИ-HE с тремя входами (рис. 3.9).

Похожие статьи