Аксиомы и тождества алгебры логики

Аксиомы

Правила для логической операции переменной величины с константой или переменной величины с самой собой или ее инвертированным значением называются аксиомами.
Обозначим некоторую переменную величину как А. Все, что верно для А, верно и для любой другой переменной величины. На рис. 4.6 изображены четыре возможные аксиомы логического умножения. Для представления
инверсии А применен нормально-замкнутый контакт. Он замкнут, если главный выключатель разомкнут. И размыкается при замыкании главного
выключателя. Таким образом, при А л А один из последовательно включенных ключей всегда разомкнут и в линии имеет место разрыв (0).
Представление аксиом алгебры логики в виде простых схем очень наглядно. Также аксиомы можно изобразить в виде таблиц истинности (рис. 4.7).
Аксиомы для логической операции сложения ИЛИ следуют из рис. 4.8. Операцию ИЛИ можно изобразить в виде параллельного включения контактов.
Если переменная инвертируется и затем еще раз инвертируется, то она принимает первоначальное значение (рис. 4.9). Два штриха инверсии над переменной не меняют ее состояния.
Девять аксиом пронумерованы от 1 до 9. Под этими номерами они далее приводятся в сборнике формул.

Законы коммутативности и ассоциативности

Закон коммутативности еще называют переместительным законом. Он применяется для логического сложения и умножения и интуитивно понятен из схем на рис. 4.10 и 4.11.
Результат операции логического умножения И не зависит от порядка обработки переменных.
Результат операции логического сложения ИЛИ не зависит от порядка обработки переменных.

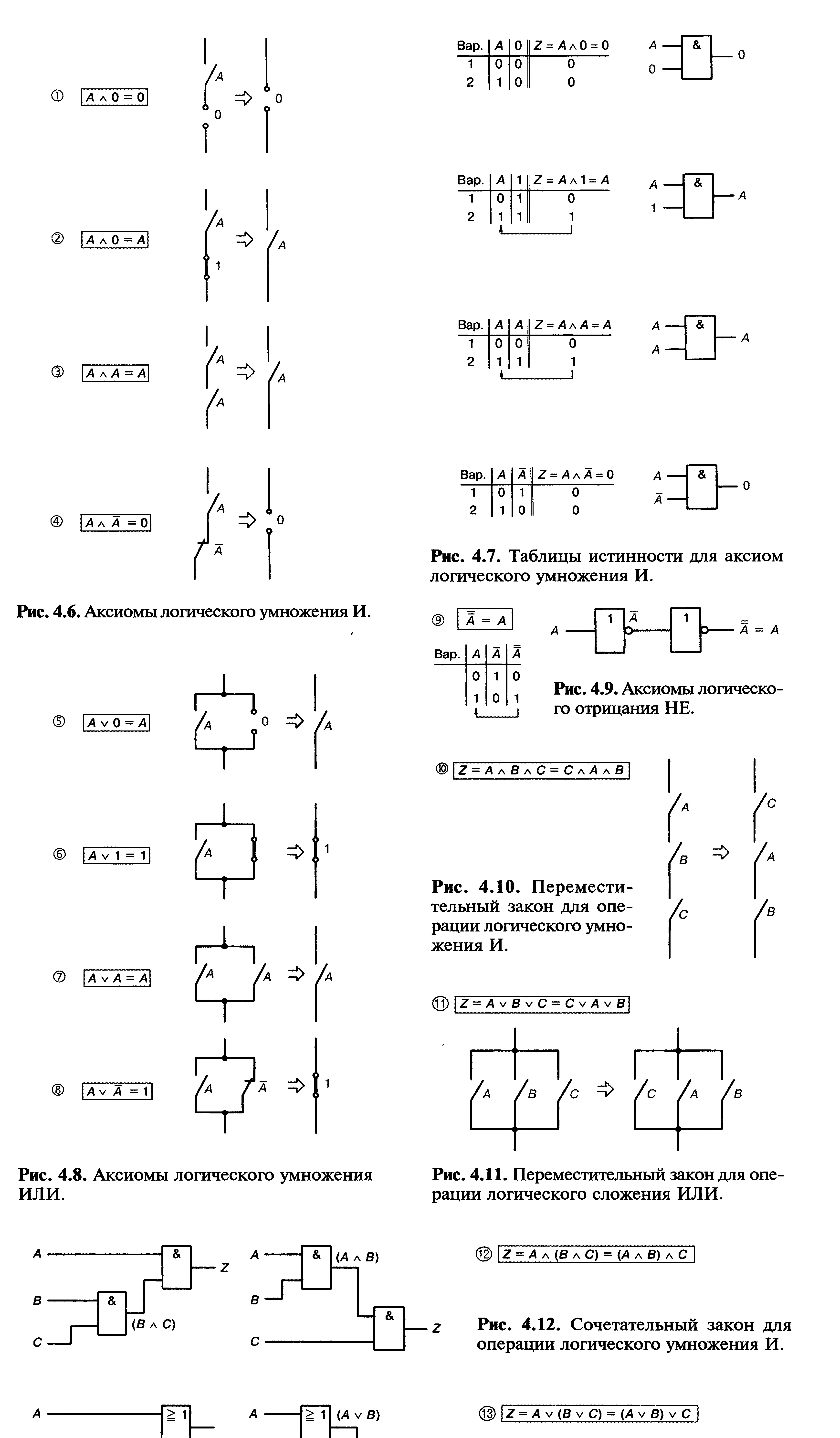
Рис. 4.6. Аксиомы логического умножения И.
Рис. 4.7. Таблицы истинности для аксиом логического умножения И.
Рис. 4.9. Аксиомы логического отрицания НЕ.
Рис. 4.10. Переместительный закон для операции логического умножения И.
Рис. 4.8. Аксиомы логического умножения «ИЛИ».
Рис. 4.11. Переместительный закон для операции логического сложения «ИЛИ».
Рис. 4.12. Сочетательный закон для операции логического умножения «И».
Рис. 4.13. Сочетательный закон для операции логического сложения «ИЛИ».

Закон ассоциативности еще называют сочетательным законом. Он применяется для логического умножения (рис. 4.12) и сложения (рис. 4.13).
Результат операции логического умножения «И» не зависит от порядка обработки переменных.
Результат операции логического сложения ИЛИ не зависит от порядка обработки переменных.

Дистрибутивный закон

Дистрибутивный закон также называют распределительным законом. Распределительный закон логического умножения по отношению к сложению играет большую роль на практике при преобразовании логических выражений.
Различают конъюнктивный распределительный закон и дизъюнктивный распределительный закон. Конъюнктивный распределительный закон записывается как
Z = А А (В V С) = (Л А В) V (А а С).
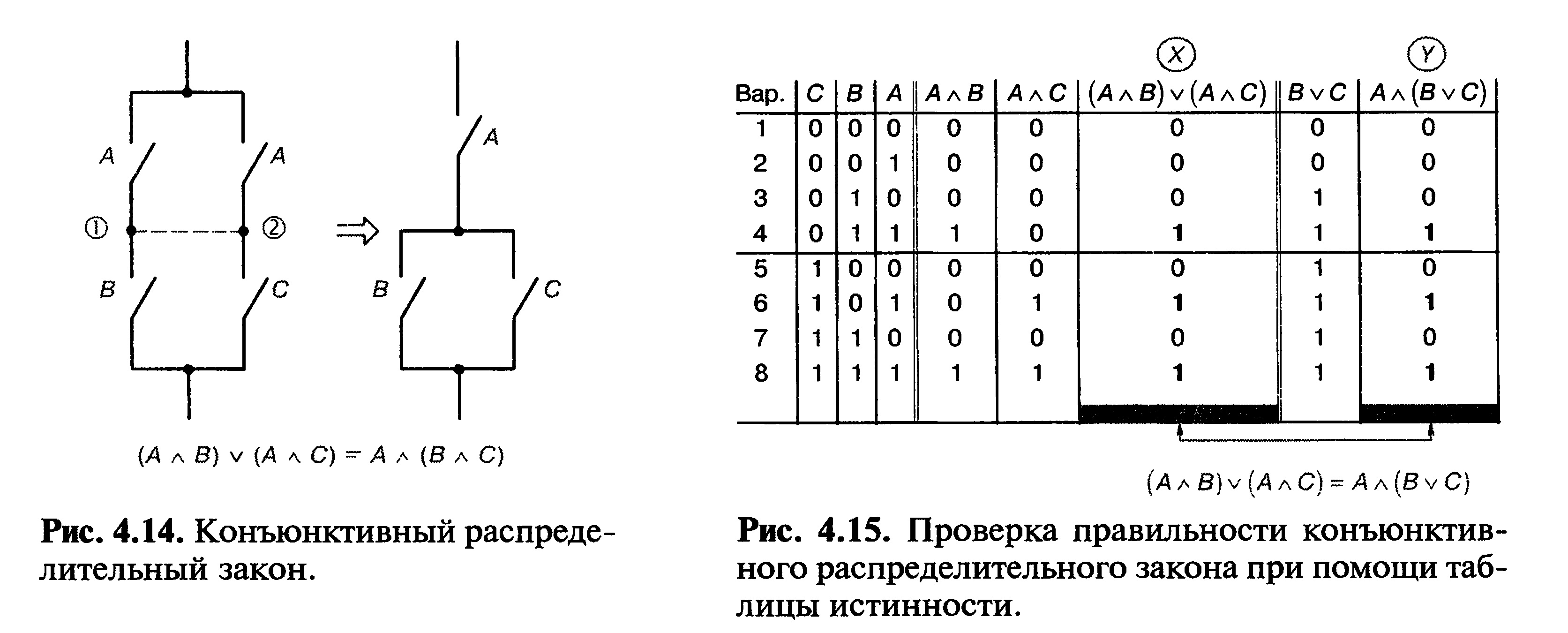
Переменная А в операции логического умножения И «распределяется» по переменным Б и С. Схема на рис. 4.14 доказывает правильность этого тождества. Так как оба контакта А могут коммутироваться только одновременно, узлы 1 и 2 можно соединить без изменения действия схемы.
Чтобы еще лучше пояснить этот закон, тождество проверяется таблицей истинности (рис. 4.15). Состояния переменных в колонках Xu Yодинаковы. Значит, конъюнктивный распределительный закон верен.
Дизъюнктивный распределительный закон записывается как

Z = A v (Б л С) = (A v 6) л (A v С).
Переменная А в операции логического сложения ИЛИ «распределяется» по переменным В и С. Схема на рис. 4.16 доказывает правильность этого тождества. Так как оба контакта А могут коммутироваться только одновременно, схему можно преобразовать, как это изображено на рис. 4.16, без изменения действия схемы.

Советуем самостоятельно проверить последнее тождество таблицей истинности аналогично таблице на рис. 4.15.
Покажем применение дизъюнктивного распределительного закона на примере. Упростим выражение
Z = (К v Л/)л(К v М).
Согласно дизъюнктивному распределительному закону оно преобразуется:
Рис. 4.16. Дизъюнктивный распределительный закон.
(Av B)a(AvC)=Av(B л С)
Z = (К v М) л (К v М) = К v (М л М).
Выражение МлМ является логическим сложением переменной и ее инвертированного значения. По аксиоме 4 на рис. 4.6 это выражение дает результат 0:
Согласно аксиоме 5 (рис. 4.8) выражение (переменная v 0) равно переменной
Z = K.

Теоремы де Моргана

Английский математик де Морган (1806—1871) дополнил аксиомы алгебры логики теоремами, названными в его честь. Теоремы де Моргана имеют большое практическое значение при упрощении инвертируемых выражений для логических операций с элементами И-НЕ и ИЛИ-HE. Существуют две теоремы де Моргана.
Первая теорема де Моргана:
Z = АлВ = AvB.
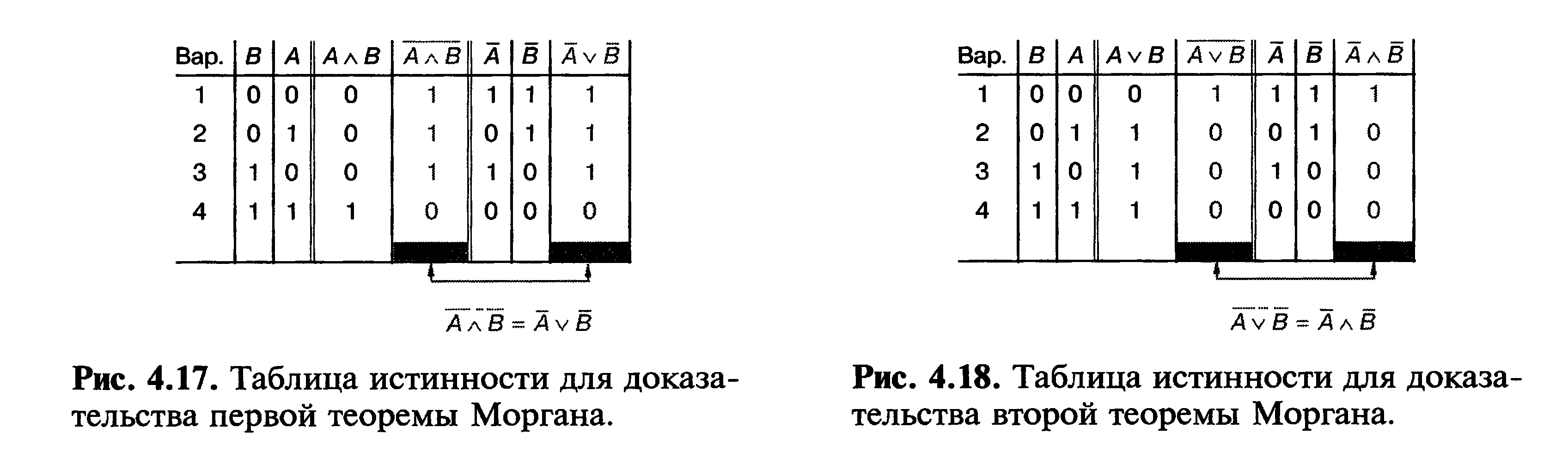
Эта теорема доказывается с помощью таблицы истинности (рис. 4.17). Вторая теорема де Моргана:
Z = Av В = А л В.
Согласно теоремам взаимно меняется тип логической операции (И и ИЛИ). Вторая теорема доказывается с помощью таблицы истинности (рис. 4.18).

Покажем важность теорем де Моргана на примере. С их помощью можно значительно упростить выражение:
P = RaSvRaS.
Первая часть уравнения RaS согласно первой теореме преобразуется в Rv S. Вторая часть уравнения RaS согласно той же теореме преобразуется в Rv S. R согласно аксиоме 9 равно R.
P = RaSvRaS;
Р = Rv S v Rv S;
Р = Rv S v Rv S.
Последовательность переменных изменена. Проведем преобразования по аксиомам 8, 7 и 6:
1 v А = 1
Р= 1
Теоремы де Моргана действуют также и для логических операций с большим количеством переменных:
Z = 4a6aCaDa... = j4vBvCvDv...
Z = AvBvCvDv... = AaBaCaDa...
Задание -------------------------------------------------------------
Составьте таблицу истинности и проверьте истинность теоремы де Моргана для трех переменных.

Приоритеты логических операций

Логическая операция И и ИЛИ с несколькими переменными может привести к неоднозначности. Уравнение
Z = A v В а С
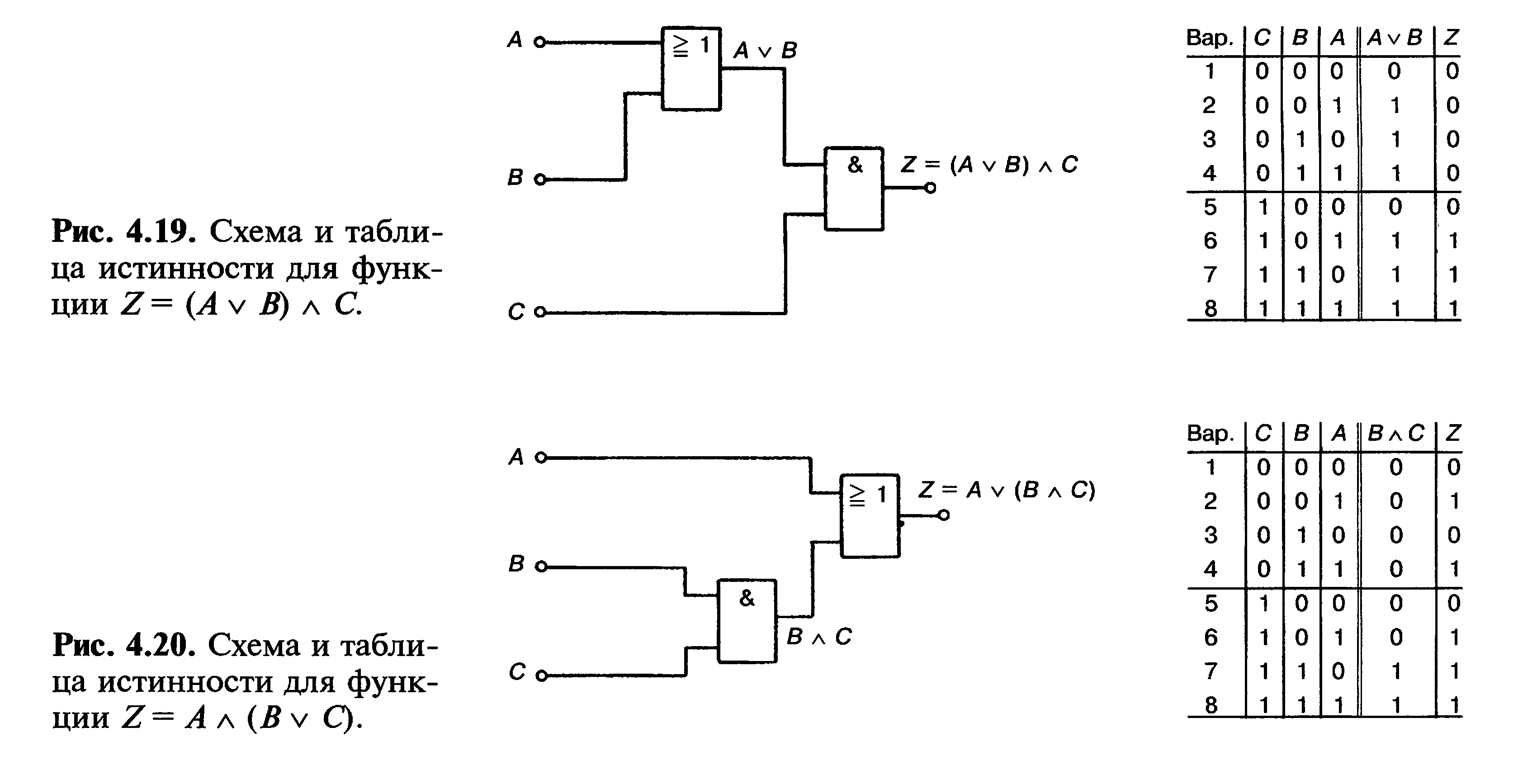
может быть решено двумя способами. Можно сначала сложить переменные А и В, затем умножить результат на С. Соответствующая схема и таблица истинности изображены на рис. 4.19.
С другой стороны, можно сначала перемножить переменные В и С, а результат сложить с А. Соответствующая схема и таблица истинности изображены на рис. 4.20. Zb этих двух вариантах является результатом абсолютно разных логических операций. Неоднозначность можно устранить с помощью скобок. В первом случае нужно писать Z = (A v В) а С. Во втором случае — Z = A v (В а С).

От скобок можно отказаться, если ввести приоритеты логических операций.
Логическая операция с более высоким приоритетом выполняется перед другими логическими операциями. Приоритет существует и в обычной алгебре. Умножение и деление имеют там более высокий приоритет перед сложением и вычитанием.
В алгебре логики более высокий приоритет имеет операция логического умножения И.
Операция логического умножения И выполняется перед логическим сложением ИЛИ.
Z = A v В л С =Ф Aw {В а С).
Теперь рассмотренное выше уравнение становится однозначным.
Если в выражении алгебры логики присутствуют операции логического умножения и сложения, то переменные, связанные логическим умножением, должны читаться так, как будто взяты в скобки.

Похожие статьи