Таблица истинности и цифровая схема

В разделе 2.2 с помощью таблиц истинности были определены логические функции схем, составленных из нескольких основных логических элементов. И так же, как для нескольких последовательно включенных элементов можно определить таблицу истинности, ее можно определить для любой цифровой схемы, состоящей из большого числа логических элементов.
Для любой цифровой схемы существует таблица истинности.

Таблица истинности цифровой схемы с двумя входами

Составим таблицу истинности для цифровой схемы на рис. 3.1. Таблица истинности позволяет определить, какие логические операции выполняет данная схема.
Так как схема имеет два входа (А, В), возможны только 4 варианта. Номера вариантов и комбинации состояний входов для А и В записываются по ранее описанной схеме (рис. 3.2).

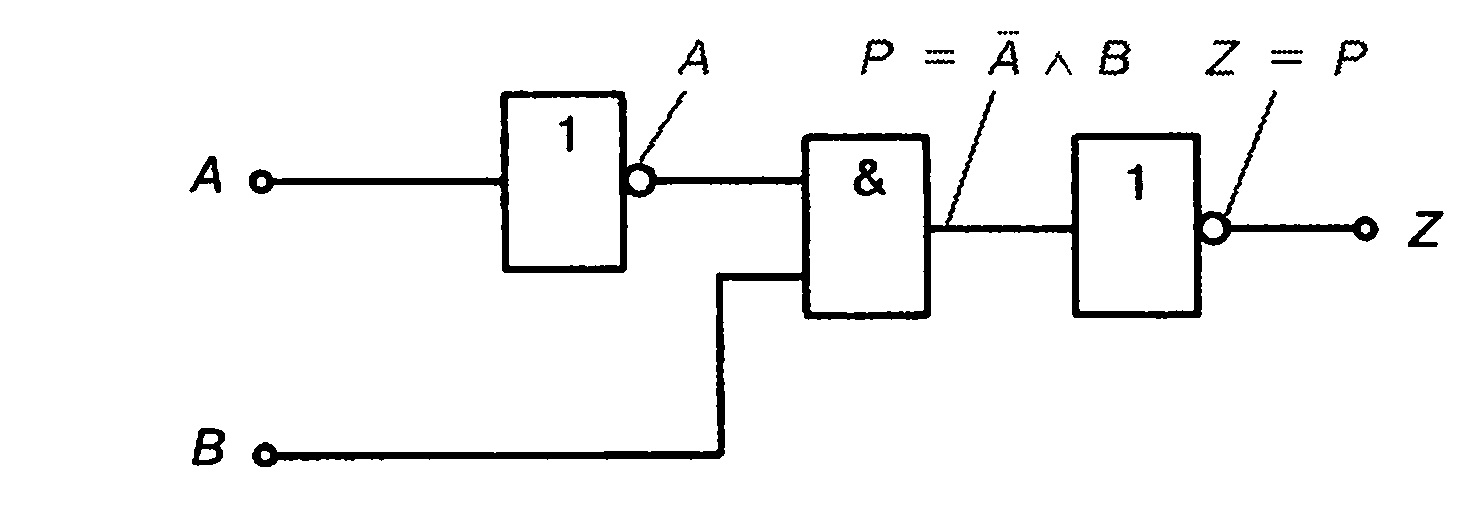
Рис. 3.1. Цифровая схема

Первый элемент является элементом НЕ. Если состояние его входа обозначить как А, то на выходе будет инвертированное значение А. Четвертый столбец таблицы истинности содержит инвертированные значения А (обозначено серым на рис. 3.3). Если в варианте А = 0, то А = 1. Это варианты 1 и 3. Если в варианте А = 1, то А = 0. Это варианты 2 и 4.
Вход элемента И (второго элемента) имеет обозначение А, другой вход
обозначен как В. Логическое умножение происходит между состояниями А и В. Соответствующие столбцы в таблице истинности (рис. 3.3) подчеркнуты серым. Выход элемента И обозначен как Р, для которого верно равенство:
Р = АлВ.
Р равно 1 только тогда, когда как А = 1, так и В = 1. Это верно только для варианта 3. Значит Р = 1 только в третьем случае, а для всех других Р = 0 (рис. 3.3).
На входе третьего элемента (НЕ) находится состояние Р, выход обозначим как Z. Так как этот логический элемент инвертирует состояние Р,
то Z— Р. Из 0 в P-столбце будет 1 в Z-столбце. Z-столбец является столбцом результата. В нем находится результат логической функции цифровой схемы.
Для Z можно записать следующие уравнения:
Z = Р;
Z = А л В (так как Р = А а Д).
Эти уравнения описывают принцип действия схемы или, другими словами, логическую функцию, которую она реализует.

Таблица истинности цифровой схемы с тремя входами

Составим теперь таблицу истинности для цифровой схемы с тремя входами (по рис. 3.4).
Цифровая микросхема с тремй входами имеет 8 вариантов. Номера вариантов и комбинации состояний входов для А, В и С записываются по
ранее описанной в разд. 2.3 схеме (рис. 3.5). Для А и В предусмотрены два столбца.

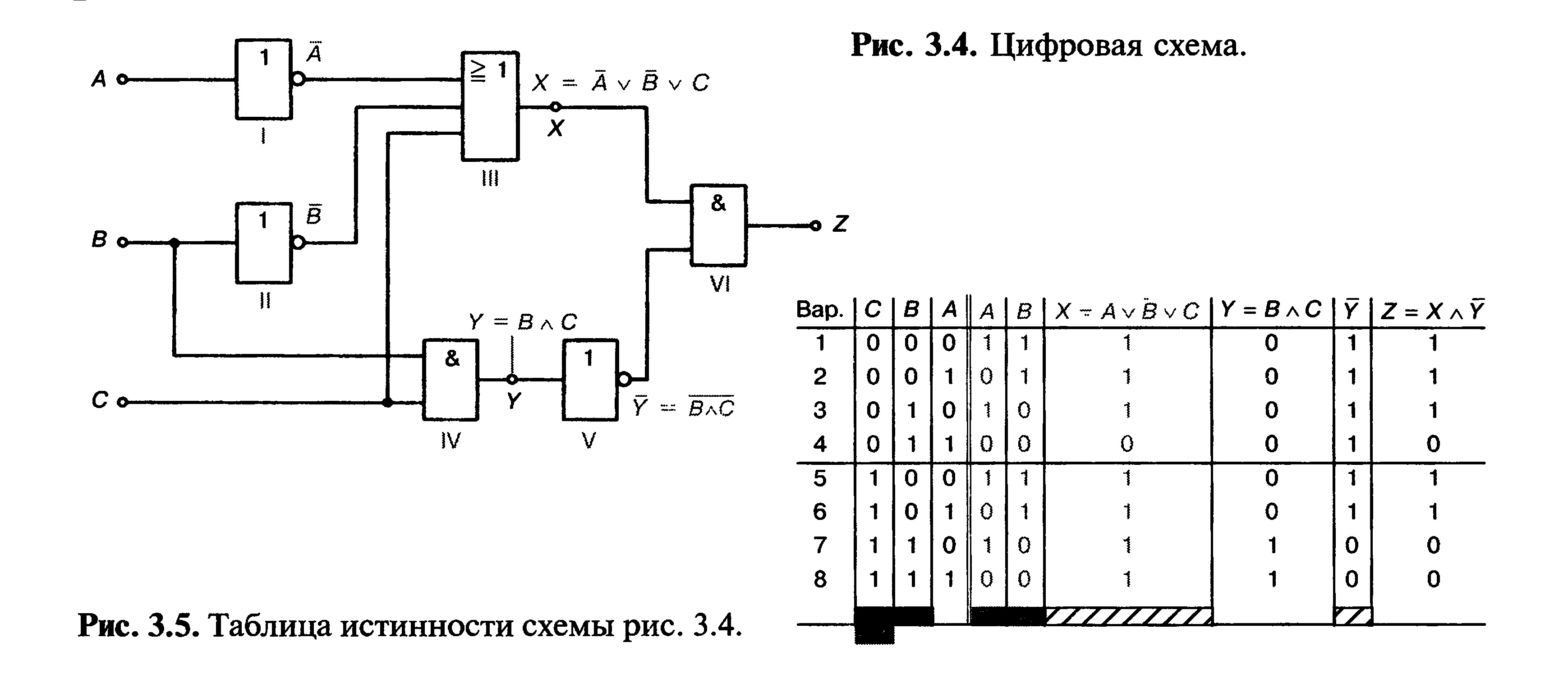
В столбце А находятся состояния, инверсные состоянию А (из 0 будет 1, из 1 будет 0).
Входы элемента ИЛИ обозначены А, В, С. Содержимое этих трех столбцов логически складывается. На выходе X появляется состояние логической 1 в том случае, если по меньшей мере состояние одного входа равно 1.
Три рассматриваемых столбца подчеркнуты на рис. 3.5 серыми полосами. Для случая 1 Х= 1, так как А = 1 и В = 1. Также X— 1 в случае 2, так как здесь В = 1. Пройдя все варианты, мы устанавливаем, что только в случае 4 X имеет состояние 0. Во всех других случаях Х= 1.
Следующий столбец в таблице истинности предназначен для Y. Y является результатом логического умножения В и С. Теперь рассматриваем только столбцы В и С. На рис 3.5 они подчеркнуты черным. Убудет равен 1 только в случаях, в которых как В, так и С имеют состояние 1. Это варианты 7 и 8.
Y в свою очередь является входом элемента V, и этот элемент является вентилем НЕ. Состояние Y должно инвертироваться. Выход элемента V
обозначим как Y. Для Y предусмотрен свой столбец в таблице истинности, заполненный соответствующими состояниями.
Элемент VI является вентилем «И» с входами X и Y То есть состояния X
и Y подвергаются операции логического умножения. Соответствующие колонки на рис. 3.5 обозначены заштрихованными полосами. Выход Z= 1,
только если Х= 1 и Y = 1. Это происходит в случаях 1, 2, 3, 5 и 6.
Для Z можно записать уравнение алгебры логики, которое образуется из:
Z = Х л?, X = AvBvC;
Y = В л С (так как Y = В л С);
Z = {Av В v С) л В л С. '
Это уравнение отражает логическую функцию схемы.
Рекомендуется потренироваться в составлении таблиц истинности по заданиями из разд. 3.4.

Похожие статьи